Часто в интернет среде от диванных критиков на подобные фотографии, как фотография слева, можно увидеть кучу комментариев по типу тех, что представлены ниже.
И конечно, это ещё полбеды, что люди могут чего-то не знать, беда скорее в том, что они уверены в том, что всё знают и не пытаются выяснить правду, выдавая за неё своё неверное, ни на чём не основанное мнение.
Когда я впервые увидел такие фотографии городских «прострелов» на фоне Луны и Солнца, первое, что я подумал: «А как такое возможно? А как такое снимается?». И все дело оказалось в длиннофокусной оптике, то есть в оптике, которая работает аналогично подзорной трубе (или биноклю) и визуально увеличивает находящиеся далеко предметы.
Позже меня очень увлечет подобный жанр фотографии, что я преисполнюсь в нём настолько, что аж буду устраивать мастер классы и напишу целую книгу-гайд по тому, как планировать и делать подобные съемки максимально качественно и грамотно. На данная статья не об этом, а о том, почему такие снимки не являются «фотошопом» или склейкой кадров или монтажом/коллажем.
К сожалению, чтобы понять полностью эту статью, надо обладать базовыми знаниями школьной геометрии и чуть-чуть физики. Но на самом деле всё очень просто.
Перед тем, как переходить к теории, давайте я продемонстрирую, что вообще происходит с увеличением фокусного расстояния объектива, что фактически и есть просто оптическое увеличение или, если говорить простым языком, визуальное приближение объекта к нам.
На примере слева на верхнем кадре показано, как выглядит Исаакиевский собор в Санкт-Петербурге на объектив с фокусным расстоянием в 100 мм. Давайте думать, что так, например, снимает и видит данный пейзаж камера вашего телефона. Согласитесь, собор находится очень далеко и выглядит довольно маленьким.
А теперь давайте с помощью цифрового зуммирования на вашем телефоне в шесть (6х) раз увеличим данный кадр и получим кадр представленный посередине. Да, качество такого кадра оставляет желать лучшего, но теперь собор занимает больше места на фотографии. Тоже самое произошло бы с Луной и Солнцем, но тут начинает играть первостепенную роль расстояние до объекта и размер этого объекта. Об этом чуть подробнее будет рассказано далее.
Ну и последний нижний кадр сделан уже не с помощью цифрового увеличения, а с помощь оптического, на объектив с фокусным расстоянием в 600 мм. Проще говоря, снят на подзорную трубу. При его сравнении со средним кадром вид объектов и их расположение не поменялось. Изменилось только качество в лучшую сторону.
Также обратите внимание, что при взгляде через длиннофокусную оптику или опять же, например, через бинокль или подзорную трубу, начинает казаться, что фон приближается к объекту, а все объекты будто-то бы начинают становиться больше и визуально располагаться рядом друг с другом. Такой эффект называется сжатием перспективы. Он происходит с удалением наблюдателя от объекта.
Теперь давайте немного углубимся в теорию данного оптического явления.
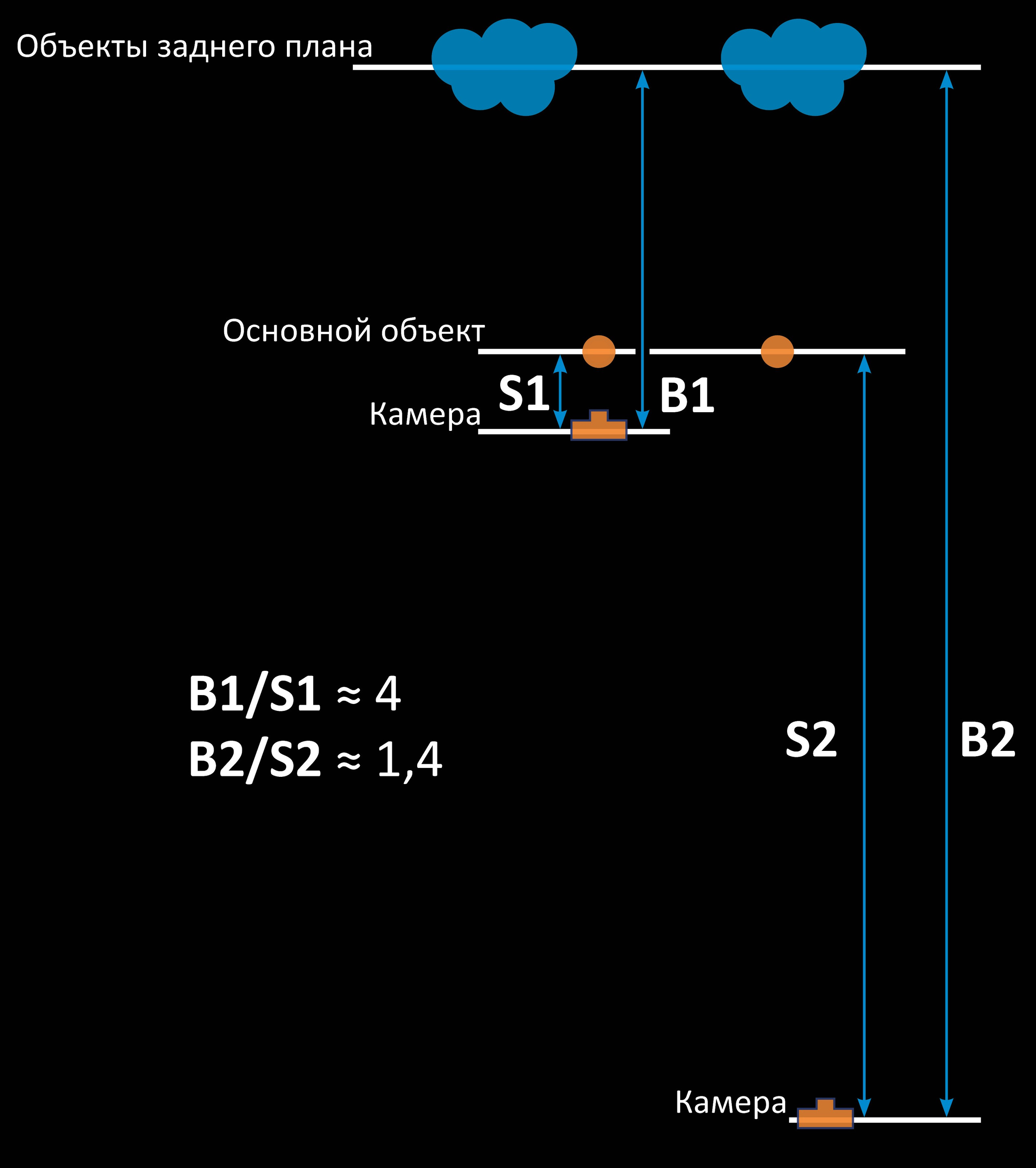
Обратите внимание на схему справа. С математической точки зрения сжатие перспективы можно описать как изменение отношения расстояния B (камера — объекты заднего плана) к расстоянию S (камера — основной объект) с удалением от самих объектов. А само отношение B/S — это ничто иное, как коэффициент подобия фигур из геометрии 8ого класса.
Чем сильнее будет приближаться отношение B/S к единице, тем сильнее будет эффект сжатия перспективы. Например, при B1/S1 ≈ 4, основной объект будет выглядеть большим, а объекты на заднем плане ощущаться маленькими и более удаленными. А при B2/S2 ≈ 1,4 размеры основного объекта и объектов на заднем плане уже будут почти такими, как если бы они находились в одном месте рядом друг с другом.
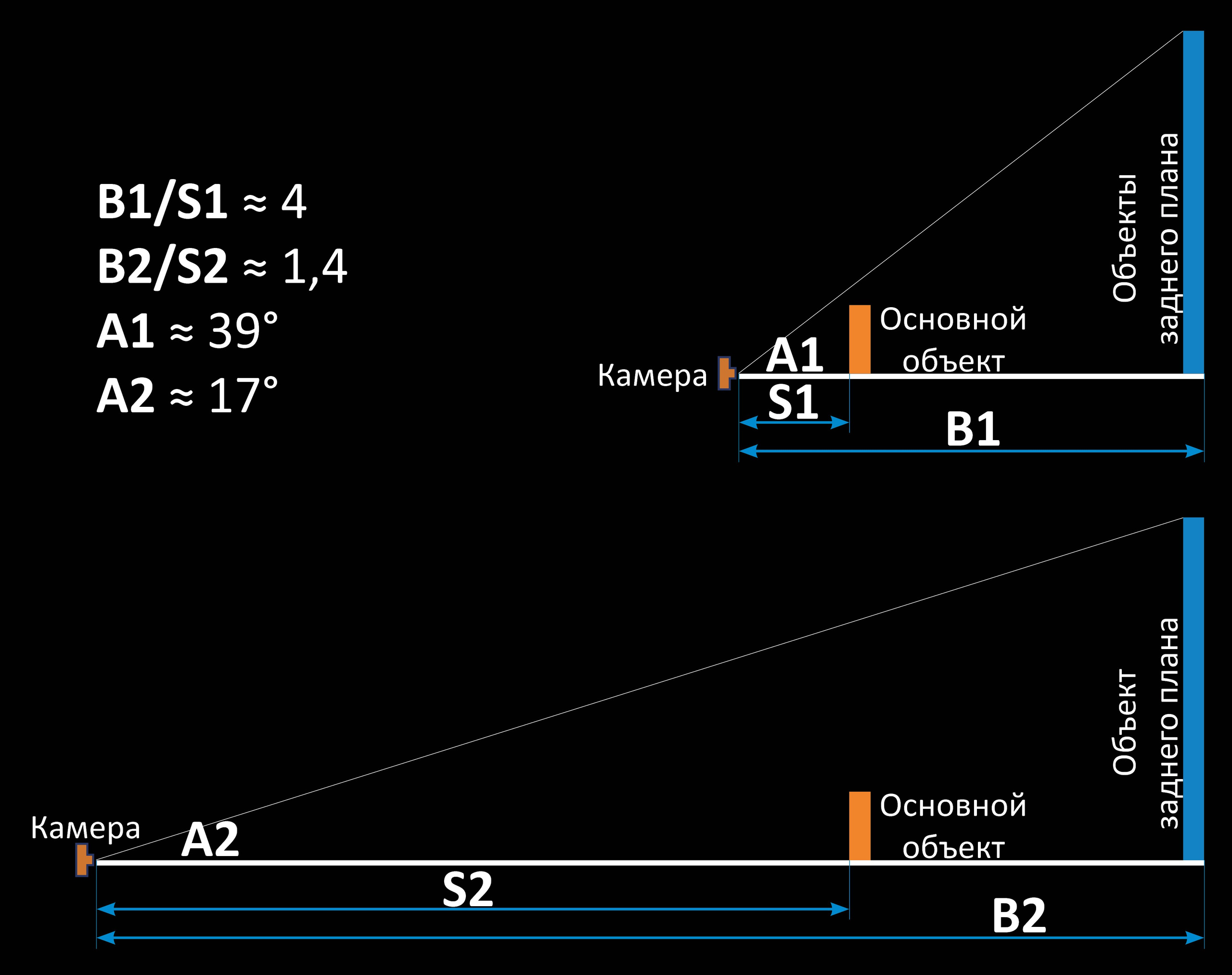
Для большего понимания продемонстрируем это на ещё одной схеме слева, в которой уже будет фигурировать угол обзора.
На схеме объект заднего плана в 5 раз выше основного, а коэффициенты подобия аналогичны первой схеме. Даже схематически по углу обзора A1 видно, что объект заднего плана при B1/S1 ≈ 4 будет выглядеть немногим выше, чем основной. А если быть точным, то его размер будет 5/4 = 1,25 от размера основного. То есть, если, например, основной объект обладает высотой 100 м, то визуально при таких параметрах съемки объект заднего плана будет выглядеть так, как если бы он стоял рядом с основным, но был высотой не 500 м, а 125 м.
А что будет, если коэффициент подобия будет не 4, а как на втором примере 1,4? Тогда размер объекта заднего плана будет казаться как 5/1,4 = 3,57 от размера основного. То есть при высоте 100 м основного объекта, объект заднего плана будет визуально выглядеть как объект высотой 357 м. Догадываетесь к чему я клоню?
При соотношении B/S ≈ 1 размеры объектов визуально будут выглядеть так, как будто они находятся совсем рядом и более того, в таком случае мы можем даже сравнить их размеры друг относительно друга почти без перспективных искажений.
Это и есть эффект сжатия перспективы. Чем мы дальше от самих объектов, тем более близко друг к другу будут визуально располагаться объекты, и тем более визуально будут соотносится их линейные размеры друг относительно друга, как если бы объекты на самом деле находились рядом друг с другом.
Телеобъектив помогает увидеть эффект сжатия перспективы за счёт оптического увеличения и узкого угла обзора. Сам он ничего с перспективой не делает. Никакой магии и фотошопа, тривиальные геометрия и физика.
Чтобы закрепить материал в применении к реальной жизни, продемонстрирую с помощью программы PlanIt Pro справа, как будут выглядеть, Исаакиевский собор (высота 102 м) и Лахта-Центр (высота 462 м) в Санкт-Петербурге на одной линии друг относительно друга при уменьшении коэффициента подобия — увеличения расстояния от точки наблюдения до объектов, а ниже продемонстрирую пару моих работ с этими объектами.
Представленные слева работы — это не фотошоп, а реальные фотографии, если говорить о расположении объектов друг относительно друга и того, как они выглядят.
Но фотошоп тут есть, это «включение» архитектурной подсветки у зданий во время заката — такой прием обработки называется композитная фотография или TimeBlending, суть которого в том, чтобы совместить два одинаковых по композиции кадра, но снятых в разное время, например, один во время заката, а другой в момент, когда включены архитектурная подсветка и уличное освещение, но это не тема данной статьи.
Всё ещё не верите что эти кадры реальны и такой вид, хоть и через подзорную трубу, но существует? А что если я покажу вам ниже два видео с места событий во время съемок этих двух кадров?
Остается ещё один важный вопрос, так сильно будоражащий сознания интернет критиков: почему на фотографиях городских прострелов Солнце или Луна получаются таких невероятных, сюрреалистических размеров? Например, как на данных фотографиях с маяком слева и справа.
И сразу скажу, что это не фотошоп, никакой магии, только физика и геометрия уровня школьной программы 8ого класса. Сейчас мы разберемся что к чему.
В прошлой теме мы оперировали понятием линейного размера объекта — размера, который можно померить линейкой. Сейчас же нам будет необходим так называемый угловой размер объекта. Он применим и к предыдущей теме, просто для объяснения того материала в нем не было нужды.
Обратимся к Википедии: угловой размер — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя. Это понятие очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.
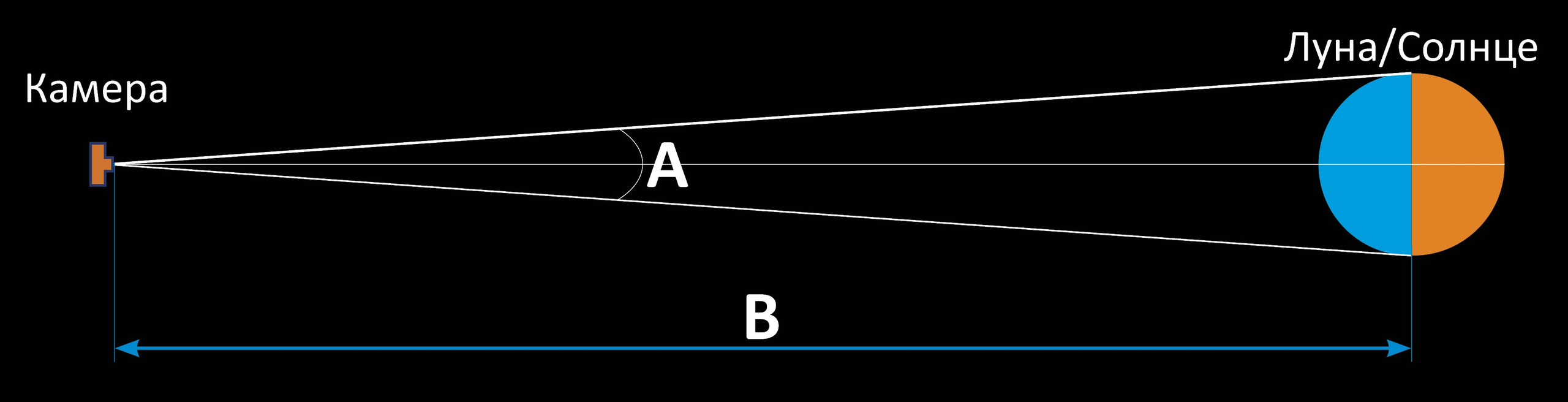
Угловой размер астрономического объекта видимого с Земли, в нашем случае Луны и Солнца, принято называть угловым диаметром (или видимым диаметром). Рассмотрим ещё одну схему ниже.
На этой схеме угол A — ничто иное как угловой диаметр Луны/Солнца в системе Земля — Луна/Солнце.
Почему мы вообще сейчас оперируем угловым размером? Дело в том, что описывать размер Луны или Солнца и то, как мы их видим с Земли с помощью линейных размеров не совсем корректно, так как они находятся от нас очень далеко, особенно в сравнении с расстоянием S до наземных (например, здания) или околоземных объектов (например, МКС).
Так как Луна движется по периодически изменяющейся эллиптической орбите, то для неё: B = 356,41 — 369,96 тыс. км в перигее (самое близкое расстояние от Луны до Земли), и B = 404,18 — 406,74 тыс. км в апогее (самое дальнее расстояние от Луны до Земли).
Земля движется по периодически изменяющейся эллиптической орбите вокруг Солнца. Но в данном случае этими изменениями можно пренебречь. Земля проходит через точку афелия (наиболее удалённая от Солнца точка орбиты планеты) в начале Июля и удаляется от Солнца на расстояние B = 152 млн. км, а через точку перигелия (ближайшая к Солнцу точка орбиты планеты) — в начале января и приближается к Солнцу на расстояние B = 147 млн. км.
Ввиду таких огромных расстояний до Луны и Солнца, значение коэффициента подобия, который мы рассматривали в прошлой теме, всегда будет очень велико. Значит, на фоне объектов для городских прострелов размер Луны и Солнца всегда будет одинаков для конкретного фокусного расстояния вне зависимости от расстояния до этих объектов и выбранной точки съемки.
Линейные размеры Луны/Солнца и объекта при таком виде съемок даже близко не будут соотноситься друг с другом. Поэтому мы оперируем угловыми размерами. Для Луны они равны от 29’20’’ до 33’32’’, а для Солнца 31’31’’ до 32’36’’. И эти значения будут постоянны при наблюдении с поверхности Земли.
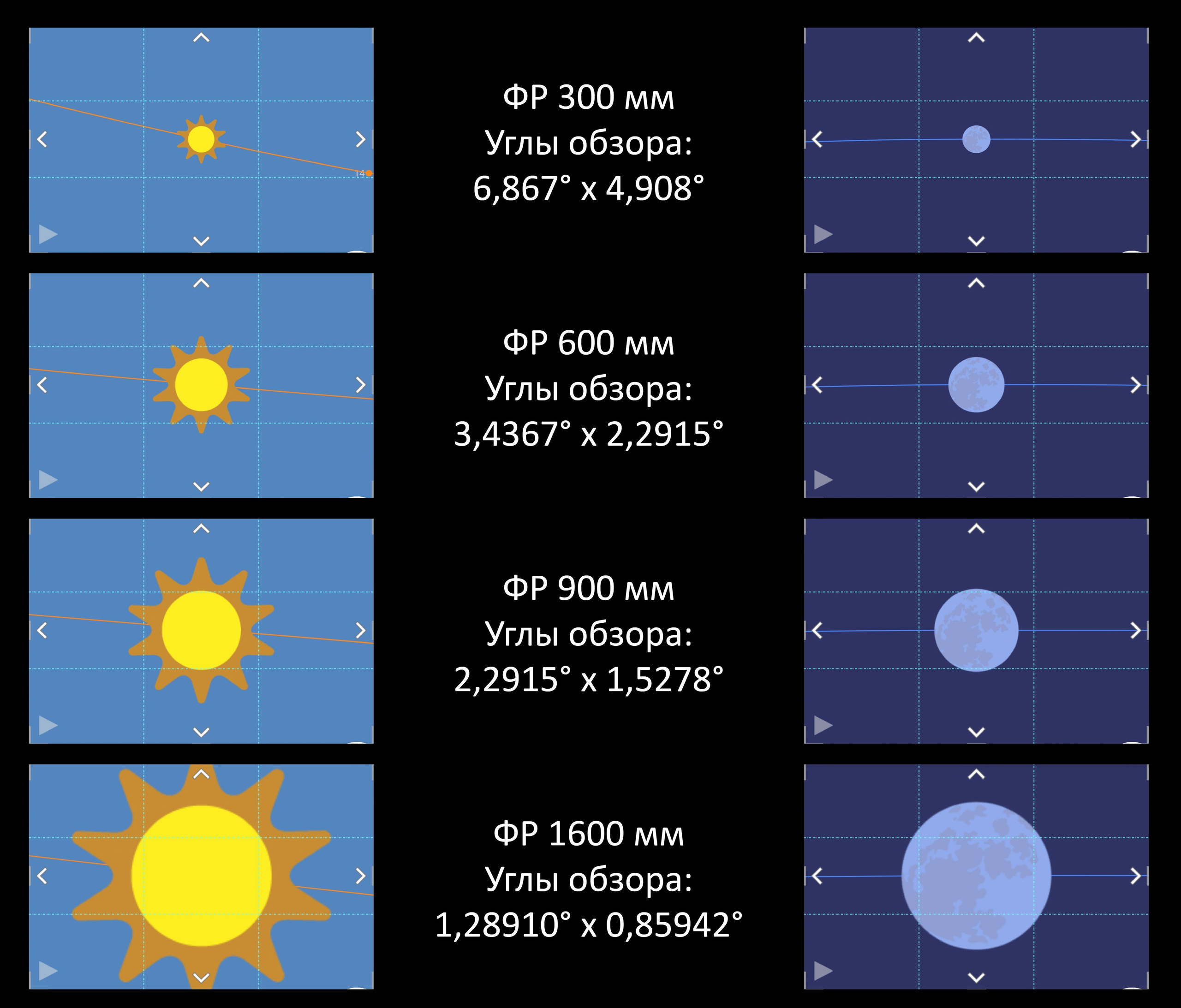
Понимаете, к чему я клоню?
Каждый объектив имеет свои углы обзора по вертикали и по горизонтали. Слева я привел несколько примеров с помощью программы PlanIt Pro различных фокусных расстояний (в пересчете на полный кадр), и то, как будут выглядеть Луна или Солнце с ними. И если мы будем использовать конкретные фокусные расстояния, или пусть для большего понимания это будут, например, разные подзорные трубы с разной степенью увеличения, то для каждого фокусного расстояния или для каждой конкретной подзорной трубы размер Луны или Солнца, которые мы будем в них наблюдать, не будет меняться, откуда бы мы их не наблюдали. А вот размер зданий, которые мы также будем в них наблюдать, как раз будет сильно меняться от расстояния до него в рамках нашей планеты. Это я, кстати продемонстрировал в примерах на фотографиях и видео выше с Лахта-центром и Исаакиевским собором
Давайте с помощью программы Planit Pro приведу на картинке справа ещё несколько примеров съемки Исаакиевского собора на фоне Луны с фокусным расстоянием 1000 мм и с различными расстояниями до собора.
Из приведённых примеров заметно, что размер Луны по мере удаления от собора остается таким же, а вот сам собор уменьшается, что вполне логично, даже несмотря на разницу в коэффициентах подобия более, чем в пять раз.
В данной системе расстояние до Луны с долей небольшой погрешности остается постоянным, или меняется менее, чем на 0,001%, что едва ли различимо.
Поэтому Луна/Солнце могут выглядеть чрезмерно большими на фоне каких-то доминант или других объектов при съемке на длиннофокусную оптику. Главное правильно подобрать расстояние от объекта до точки съемки.
В заключение данное статьи, дабы развеять все сомнения по поводу «фотошопов» таких кадров покажу вам ниже большое видео с различных съемок городских «прострелов» на фоне Луны и Солнца.
Справедливости ради скажу, что само собой бывают люди которые и вшопливают Луну или Солнце на свои фотографии, но зачастую из-за плохих знаний физики, элементарной астрономии и геометрии у человека, такие кадры выглядят нереалистично и монтаж на них очень легко выявляется.
Надеюсь, вам было интересно и вы узнали что-то для себя новое. Буду рад, если будете делиться данной статьей с диванными критиками и комментаторами, которые любят под каждой такой фотографией писать «фотошоп».
P. S. Ну, а если Вам интересно как снимать и планировать такие кадры, то вот вам мой гайд «Городские прострелы».
Статьи и гайды